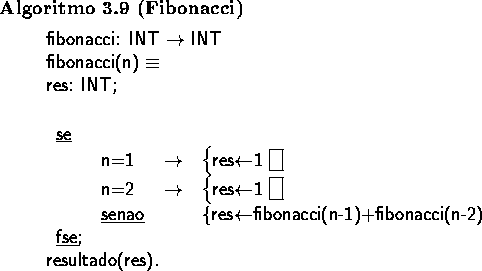O algoritmo que define uma função pode invocar outras funções. Em particular, pode invocar a própria função. Quando uma função se invoca a si mesma, diz-se que a função é recursiva. Apresentam-se de seguida dois exemplos de funções recursivas.
A função matemática factorial pode ser definida do seguinte modo:
Nesta formulação o factorial é definido à custa dele próprio, trata-se, então, de uma definição recursiva. Consideremos 3!:
Note que o valor com que se invoca o factorial vai diminuindo até chegar a zero, altura em que a recursividade termina.
Uma função para calcular o factorial obtem-se directamente da definição:

Na figura 3.2 apresentam-se as invocações geradas e os valores retornados para o cálculo de fact(4).
A série de Fibonacci foi concebida no século XIII como um modelo para a criação de coelhos. Trata-se de uma série muito simples, em que cada número é obtido pela soma dois dois anteriores:
1, 1, 2, 3, 5, 8, 13, 21, 44, ...
O problema de encontrar o n-ésimo número da série tem a seguinte formulação matemática:
Fibinacci(N) =
O algoritmo de uma função recursiva obtem-se directamente da formulação anterior: